Зуны бага сорилго №1.2

ІІ сорил: 2025 оны 6 сарын 13

Энэ сорилгыг МУИС-ийн Онолын Mатематикийн 3-р курсийн оюутан Б.Улсболдтой хамтран зохиосон болно.

Бодох хугацаа 4 цаг 30 минут.
Бодлого бүр 7 оноотой.

---

Бодлого 1

\(n\) нь натурал тоо ба \(p\) нь анхны тоо бол дараах тэгшитгэл биелэх бүх \((n,p)\) хосыг ол: \[\begin{equation*} 2^p-3=n^2-p \end{equation*}\]

---

Бодлого 2

\(xyz = 1\) байх \(x, y, z\) эерэг бодит тоонуудын хувьд дараах тэнцэтгэл биш биелэхийг батал: \[ \frac{x^3}{(1+y)(1+z)} + \frac{y^3}{(1+z)(1+x)} + \frac{z^3}{(1+x)(1+y)} \geq \frac{3}{4} \]

---

Бодлого 3

\(I\) нь \(ABC\) гурвалжинд багтсан тойргийн төв ба \(AI\) цацраг нь \(\triangle ABC\)-г багтаасан тойрогтой \(D\) цэгт огтлолцоно. \(I\)-аас \(BD\) болон \(CD\)-д буулгасан перпендикуляруудын суурийг харгалзан \(E\) болон \(F\) гэе. Хэрвээ \(IE + IF = \frac{1}{2}AD\) бол \(\angle BAC\)-г ол.

Бодолт харах

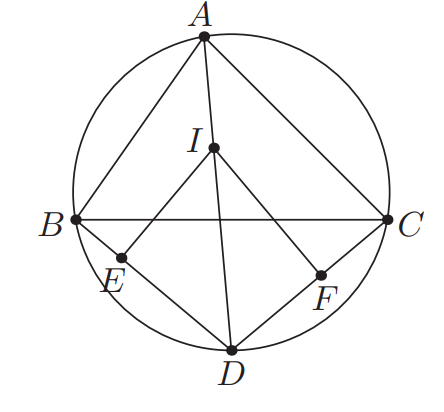
\(x = DB = DI = DC\) гэдгийг хялбар харж болно. Энэ тохиолдолд \(\angle IDE = \angle ADB = \angle ACB\) учраас \[ IE = ID \cdot \sin \angle IDE = x \sin C = x \cdot \frac{c}{2R}. \] Үүнтэй адилаар \(IF = x \cdot \frac{b}{2R}.\) Харин нөгөө талаас, Птолемейн теоремыг дөрвөн өнцөгт \(ABDC\)-д хэрэглэвэл: \[ AD \cdot a = x \cdot (b + c) \Rightarrow AD = \frac{x(b + c)}{a}. \] Эдгээрийг нэгтгэвэл: \[ \frac{1}{2} \cdot \frac{x(b + c)}{a} = IE + IF = x \cdot \frac{b + c}{2R}. \] Иймд \(a = R\) гэж гарна.

Иймээс \[ \sin A = \frac{a}{2R} = \frac{1}{2} \] гэж гарах бөгөөд энэ нь шаардлагатай бөгөөд хангалттай нөхцөл юм. Тэгэхээр боломжит утгууд нь: \[ \angle A = 30^\circ \quad \text{болон} \quad \angle A = 150^\circ. \]

---

Бодлого 4

\(\left\{a_1, a_2, a_3, \dots, a_n \right\}\) олонлог нь \(\left\{1, 2, 3, \dots, n \right\}\) олонлогийн сэлгэмэл байг. Тэгвэл \[\begin{equation*} A=|a_1 - a_2| + |a_2 - a_3| + \dots + |a_{n-1} - a_n| \end{equation*}\]

а) A-ийн хамгийн их утга хэд вэ?

б) A хамгийн их утгаа авдаг хэдэн сэлгэмэл байгаа вэ?

---