Янз бүр (5/26)
Бодлогууд
Бодлого 1 (Konhauser 2013)
Бүхэл тоонуудын хоосон биш \(S\) олонлогийг авч үзье. Хэрвээ ямар ч бүхэл \(n\) тооны хувьд дараах гурван тооны аль нэг нь \(S\)-д багтдаг бол бүгд \(S\)-д багтдаг:
- \(n\)
- \(2n + 9\)
- \(2n + 25\)
Тэгвэл \(S\) нь бүх бүхэл тоонуудын олонлог мөн үү?
Бодлого 2 (Konhauser 2013)
Тэгш өнцөгт координатын хавтгайд өгөгдсөн \(A = (4, 0), B = (0, 3), C = (0, 0)\) цэгүүдийг холбосон \(\triangle ABC\)-г авч үзье. \(P,Q\) цэгүүд нь \(\triangle ABC\)-ний тал дээр оршдог ба \(PQ\) шулуун уг гурвалжны талбай болон периметрийг хагасаар нь хуваадаг. Тийм \(P,Q\) цэгүүдийн бүх боломжит хосыг ол.
Бодлого 3 (Konhauser 2013)
\(a_0\) нь эерэг рациональ тоо. Бүх бүхэл тоо \(n \geq 0\)-ийн хувьд, \(k_n\) нь \(a_n - \frac{1}{k_n} > 0\) байх хамгийн бага эерэг бүхэл тоо байг. Хэрэв \(a_{n+1} = a_n - \frac{1}{k_n}\) бол хязгааргүй олон \(n\)-ийн хувьд \(\frac{1}{a_n}\) тоо бүхэл байж чадах уу?
Бодлого 4 (Konhauser 2024)
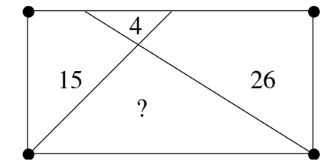
Тэгш өнцөгтийг хоёр шулуун шугамаар дөрвөн хэсэгт доор үзүүлсэнчлэн хуваав. Зураг дээрх тоонууд нь тухайн хэсгүүдийн талбай бол дөрөв дэх хэсгийн талбайг ол.
Бодлого 5 (Konhauser 2023)
\(n\) нь эерэг бүхэл тоо. Хэрвээ \(1, 2, 3, \dots, n\) тоонуудыг ямар нэгэн дарааллаар дараах нөхцөлүүдийг хангасан байхаар жагсааж болдог бол \(n\)-ийг гоё тоо гэе:
- Жагсаалтын эхний хоёр тооны дундаж бүхэл тоо
- Жагсаалтын эхний гурван тооны дундаж бүхэл тоо
- \(\dots\) гэх мэтчилэн
- Жагсаалтын бүх \(n\) тооны дундаж бүхэл тоо байдаг.
Жишээ нь: \(n = 3\) нь гоё тоо юм. Хэрвээ \(1, 3, 2\) гэж жагсаавал:
- Эхний хоёр тоо \(1\) ба \(3\)-ийн дундаж нь \(\frac{1+3}{2} = 2\) (бүхэл тоо)
- Уг гурван тоо \(1, 3, 2\)-ийн дундаж нь \(\frac{1+3+2}{3} = 2\) (бүхэл тоо) болно.
Бүх гоё тоо \(n\)-ийг ол.
Бодолт
Бодлого 3
\(\frac{1}{a_n}\) нь бүхэл тоо болчихвол, дараагийн бүх \(m > n\) хувьд \(\frac{1}{a_m}\) нь мөн бүхэл тоо байх болно. Хэрэв \(a_0 > 1\) бол \(k_0 = 1\) бөгөөд \(a_1 = a_0 - 1\) болно. Үүнийг давтан \(a_n \leq 1\) хүртэл 1-ийг хасна. Иймд \(0 < a_0 \leq 1\) гэж үзэж болно.
Хэрвээ \(\frac{1}{a_0}\) нь бүхэл тоо \(m\) бол \(k_0 = m+1\): \[ a_1 = \frac{1}{m} - \frac{1}{m+1} = \frac{1}{m(m+1)} \] Энэ нь дахин бүхэл тооны урвуу хэлбэр тул бүх \(a_n\) нь бүхэл тоонуудын урвуу хэвээр байна.
Харин хэрвээ \(\frac{1}{a_0}\) нь бүхэл тоо биш байвал \(a_0\)-г \(c_0/d_0\) гэж бичье. Энд \(1 < c_0 < d_0\) болон \(\gcd(c_0, d_0) = 1\). \(d_0 = qc_0 + r\) гэж үзье (\(0 < r < c_0\)). Тэгвэл:
\[ \frac{1}{q+1} < a_0 < \frac{1}{q} \Rightarrow k_0 = q + 1 \]
Тэгээд: \[ a_1 = a_0 - \frac{1}{q + 1} = \frac{c_0}{d_0} - \frac{1}{q+1} = \frac{c_0(q+1) - d_0}{d_0(q+1)} = \frac{c_0 - r}{d_0(q+1)} \]
Энд \(a_1\)-ийн хүртвэр \(a_0\)-ийн хүртвэрээс буурсан байна. Иймээс хэдэн алхмын дараа хүртвэр нь 1-д хүрч, \(a_n = \frac{1}{m}\) хэлбэрт очно.